1. Energy of electromagnetic wave
Electric field, Magnetic field는 energy를 가지고 있다.
Electric field energy density $u_E = \frac{1}{2} \epsilon_0 E^2 $이고,
Magnetic field energy density $u_B = \frac{1}{2\mu_0} B^2 $이다.
그런데 $ B_0 = E_0/C $ 이고, $ C = \frac{1}{\sqrt{\epsilon_0 \mu_0}} $ 이므로, $u_B = \frac{1}{2} \epsilon_0 E^2 $ 가 되어, electromagnetic wave의 electric/magnetic energy density가 완전히 동일함을 나타낸다.
따라서, electromagnetic wave의 전체 energy density $u_{tot} = \epsilon_0 E^2 = \epsilon_0 E B C $ 가 된다 .
단위면적에 electromagnetic wave를 보내어보자.
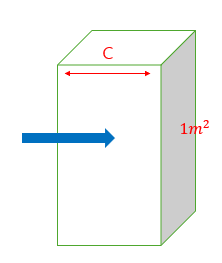
속도는 C 이므로, 초당 단위면적이 받는 energy는 $u_{tot} C = \epsilon_0 E B C = \frac{EB}{\mu_0}$ 이다.
이것을 vector로 표현한 것이 Poynting vector $ \vec{S} = \frac{\vec{E} \times \vec{B} }{\mu_0} $ $J/(m^2 sec)$이다.
그런데, electromagnetic wave는 cos/sin 의 형태이므로, Poynting vector의 평균 $ < S' > = \frac{1}{2} \frac{E_0 B_0}{\mu_0} = \frac{1}{2} \frac{E_0^2}{\mu_0 C} $ 이다. 이것은 단위면적이 초당 받는 평균적인 에너지이다.
Electric field의 증가의 제곱만큼 면적에 가해지는 에너지가 증가하게 된다.
2. Production of electromagnetic wave
charge를 빠르게 좌우로 움직이면서 가속하면, electromagnetic wave가 생성된다.
아래와 같이, charge를 매우 짧은 t초동안 가속시켜 오른쪽으로 보내보자.

t초동안, 빛의속도로 전달되는 Ct보다 먼곳까지는 어떠한 message도 도달 할 수 없다.
따라서 t초동안 가속시켜 이동시켜도 Ct밖의 전기장은 변화하지 않는다.
하지만, 동일한 크기의 electric field는 항상 연결되어있어야 하므로, 새롭게 생성된 electric field는 Ct바깥의 electric field와 연결되어 있어야 한다. 따라서, Ct내부에서는 전기장이 뒤틀리는 지점(kink)이 발생한다.
매우 빠른 frequency로 charge를 좌우로 움직이면서 가속시키면, kink가 계속적으로 발생하고, 바깥으로 빛의 속도로 전파가 되며, electromagnetic change를 생성한다. 이를 통해 우리는 electromagnetic wave를 경험하게 된다.
흥미로운 점은, 가속하는 방향에서는 kink가 발생하지 않고, electromagnetic wave도 전파되지 않는다.
또한, 가속하는 방향과 perpendicular한 plane으로 전파되는 electromagnetic wave의 크기가 가장 크다.
3. Pressure of electromagnetic wave
빛을 입자(photon)라고 생각하였을 때, photon 1개의 momentum $ p = E/C $ 로 정의된다. E는 photon 1개의 energy이다.
이러한 photon을 물체에 지속적으로 쏘면, F = dp/dt = ma 이므로 momentum보존법칙에 의해 momentum이 전달되는 시간동안 물체는 힘을 받게 된다.
Poynting vector는 단위면적에 가해지는 에너지(E)를 시간(t)으로 미분한 dE/dt 인데, 이를 속도 C로 나누면 p = E/C이므로, dp/dt가 되어 단위면적에 가해지는 힘이 된다. 단위면적에 가해지는 힘은 압력(pressure)이므로, poynting vector를 C로 나눈것은 해당 방향으로 가해지는 pressure이 된다.
참고로 이것은 모든 energy가 물체에 흡수됨을 가정한 것이고, 만약 완전히 물체를 투과한다면 pressure = 0 이다.
electromagentic wave가 완전히 반사된다면 pressure는 2배가 된다.
4. Electric field of electromagnetic wave at arbitary point
임의의 지점에서의 Electromagnetic wave에 의한 electric field를 생각해보자.

charge가 가속도 a, frequency $\omega$ 로 진동하고 있다고 해보자.
임의의 지점 P에서 Electric field $\vec{E}$ 는 $\vec{r}$ 과 perpendicular하다. 또한, vector a, r, E 는 같은 평면에 있어야 한다.
이 두 조건을 이용하면 임의의 지점에서 electric field의 방향을 찾을 수 있다.
(이러한 electric field의 방향과 수직으로 놓여진 안테나는 신호를 수신할 수 없다)
eletric field의 크기는 charge의 크기 q, 가속도의 크기 a, $sin\theta$ 에 비례하며, 거리 r에 반비례 한다.
Poynting vector는 electric field의 제곱에 비례하므로, 지점의 거리가 2배 멀어지면 전달되는 에너지는 4배로 줄어든다.
'프로그래밍 > Elecricity and Magnetics' 카테고리의 다른 글
| 28. Light polarization (0) | 2024.12.25 |
|---|---|
| 27. Snell's law & Velocity of light (0) | 2024.12.22 |
| 25. Eletromagnetic Wave (0) | 2024.12.05 |
| 24. Traveling wave & Standing wave (0) | 2024.12.01 |
| 23. RLC circuit (0) | 2024.12.01 |



