1. RLC circuit
다음과 같이 $V = V_0 coswt$ 를 제공하는 AC battery 가 연결된, RLC circuit을 생각해보자.
Faraday's law에 의해, $ \oint E \cdot dl = IR + 0 + V_C - V_0 coswt = - L \frac{dI}{dt} $ 이다. (inductance의 저항은 0)
$V_C = Q/C, I = dQ/dt $ 이므로, Capacitor의 charge Q에 대한 식으로 정리하면, $L\frac{d^2Q}{dt^2} + R\frac{dQ}{dt} + \frac{Q}{C} = V_0 coswt$ 로 쓸수 있다
해당 differential equation을 풀고, I = dQ/dt 이므로, t에 대해 미분하면 I에 대한 식을 얻게 된다.
최종식(steady-state solution)은 다음과 같다.
$ I = \frac{V_0}{\sqrt{R^2+ X^2}} cos(\omega t-\phi) $, $tan(\phi) = X/R $
여기서 $ X = \omega L - \frac{1}{\omega C} $ 이고, reactance라고 한다.
$ Z = \sqrt{R^2+ X^2} $ 는 impedance라고 한다. impedance는 실제 유효저항이며, R, L, C 값에 의존한다.
$ \frac{V_0}{\sqrt{R^2+ X^2}} $ 은 maximum current인 $ I_{max} $이다.
참고로, $ X = \omega L - \frac{1}{\omega C} = 0 $ 일 때, $ \omega_0 = \frac{1}{\sqrt{LC}} $ 이며, resonance frequency라고 한다. 이 때, I는 최대가 되며, $ \phi = 0 $ 이다 .
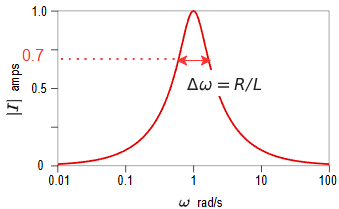
참고로, $ \omega $ 에 따른 current의 그래프를 그렸을 때, $ \omega = 0 $ 일 경우, DC battery를 연결한 것과 같으므로, steady-state에서 I = 0 이다. $ \omega = \infty $ 일 경우, impedance가 무한대가 되어 I = 0 이 된다. 따라서, 그래프는 위와 같은 그래프가 된다.
그래프가 더 뾰족할 수록, 특정 Input frequency에 대해서 circuit이 반응성이 높아짐을 의미하는데, circuit의 Quality $Q = \frac{\omega_0}{\Delta \omega} = \frac{1}{R} \sqrt{\frac{L}{C}} $ 이다.
즉, quality를 높이려면 L을 크게하고, R, C를 작게하면 된다.
Quality Q값이 클수록, resonance frequency이외의 input에 대해서는 current가 거의 흐르지 않으므로, resistance에 의한 energy lost가 매우 적고, resonance frequency에 가까워지면 갑자기 current가 급증하게 된다.
2. Metal detector
Metal detector는 두 RLC circuit이 놓여있고, 서로의 current의 변화가 magnetic field변화를 야기하고, 서로의 current에 영향을 주도록 놓여져있는 것을 생각하면 된다. 두 RLC circuit는 resonance frequency로 설정되어 있다가, metal과 같은 eddy current가 발생할 수 있는 물체가 놓여지면, 둘 사이에 교묘하게 맞추어진 resonance가 깨져 alarm이 울리게 된다.
'프로그래밍 > Elecricity and Magnetics' 카테고리의 다른 글
| 25. Eletromagnetic Wave (0) | 2024.12.05 |
|---|---|
| 24. Traveling wave & Standing wave (0) | 2024.12.01 |
| 22. RC circuit & Transformer (0) | 2024.11.28 |
| 21. Hysteresis curve & Maxwell equation (0) | 2024.11.26 |
| 20. Magnetic Materials & Dia / Para / Ferromagnetism (0) | 2024.11.19 |




