1. Grad V
임의의 Electric field가 존재하고, 임의의 point A로부터 임의의 경로를 따라 다시 point A로 옮겼을 때, electric potential은 변화가 없다. 이것을 수식으로 쓰면 다음과 같다.


Electric field와 Electric potential간에는 다음과 같은 관계가 있다.
charge +Q와 r만큼 떨어진 위치에서, 그에 의한 Electric field는

그에 의한 Electric potential은

따라서, potential의 derivative의 크기가 electric field가 된다.

Electic field와 수직방향으로 움직일 경우, potential은 변화하지 않는다. 그러한 경로가 바로 equipotential line인데, 이것은 equipotential line과 electic field는 항상 perpendicular하다는 의미와 같다.
위의 수식에 따라, Euclidean coordinates에서 3차원의 Electric field는 다음과 같이 기술될 수 있다.
x방향의 Electric field는, yz의 변화를 constant로 놓은 V에 대한 x방향의 differential이다.
y방향의 Electric field는, xz의 변화를 constant로 놓은 V에 대한 y방향의 differential이다.
z방향의 Electric field는, xy의 변화를 constant로 놓은 V에 대한 z방향의 differential이다.
Electric field는 각 differential의 vector합이므로 다음과 같이 쓸 수 있다.

Gradient function을 사용하여 표현하면,

2. Conductors
다음과 같은 static상태이며, + charge인 solid conductor가 있다고 해보자.

Charge의 distribution은 어떻게 될 것인가? 그것은 gauss surface를 설정함으로서 쉽게 구할 수 있다.
solid conductor 내부에 원형 모양의 작은 gauss surface를 잡아보자.
static 상태이므로 charge는 움직이지 않고, 따라서 내부의 Electric field = 0 이라는 것을 알 수 있다.
즉, static 상태에서 내부에 charge는 존재하지 않고, 오직 surface에만 존재하게 된다.

이제 안쪽이 비워져있는 solid conductor를 생각해보자.

conductor내부에는 charge가 없는 것은 확실하다. 그렇다면, 안쪽 방향의 surface에도 charge가 존재할 것인가?
이것도 gauss surface를 설정함으로서 쉽게 구할 수 있다.

다음과 같이 gauss surface를 잡으면, static상태이므로 guass sufrace의 Electric field는 모두 0 이고, 따라서 surface내부의 charge는 0이 되어야 한다. 따라서, 외부의 표면에만 charge가 존재함을 알 수 있다.
내부의 Electric field = 0 이므로 내부의 이동의 work = 0이고 모두 equipotential하다. 따라서, surface의 charge에 의해 외부로 나가는 Electric field는 equipotential line과 수직해야하므로, sufrace에 수직한 방향이 된다.

3. Electrostatic shielding
안쪽공간이 비워져있는 conductor의 외부공간에 charge를 놓아보자.
conductor내부의 charge는 외부의 Electric field에 따라 매우매우 빠른 속도로 이동하여 내부는 static상태로 바뀔 것이고, 내부의 Electric field = 0 이 될 것이다. 따라서, 내부에서는 외부에서 어떤일이 일어나고 있는지 알지 못하는데 이것을 electrostatic shielding이다.
이번에는 안쪽공간이 비워져있는 sphere conductor의 안쪽공간에 charge를 놓아보자.
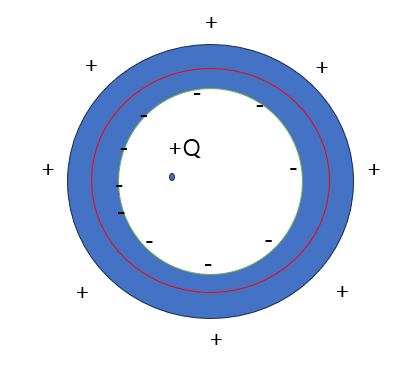
위와 같이 gauss surface를 설정하면 conductor내부의 Electric field = 0 이므로, 내부의 charge는 0이여야 한다. 즉, conductor 내부에서 이동된 - charge 와 +Q의 합은 0이 되어야 하고, conductor의 안쪽에도 charge가 존재함을 알 수 있다.
물론 +Q와 가까운 쪽에 더 많은 - charge가 쏠리게 된다. 하지만, 외부에서 보았을 때는 +Q의 위치를 이동시키든 상관없이 conductor 외부의 surface에 charge가 uniformly distributed된 것으로 보인다. 이것은 내부의 따라서 외부에서는 내부에서 어떤일이 일어나고있는지 알지 못하는데 이것은 electrostatic shielding이다.
물론 매우 빠르게 변화하는 Electric field(not static)에서는 electrostatic shielding이 잘 동작하지 않는다.
'프로그래밍 > Elecricity and Magnetics' 카테고리의 다른 글
| 7. Capacitance (0) | 2024.06.22 |
|---|---|
| 6. High-voltage breakdown & Lightning (0) | 2024.06.15 |
| 4. Electrostatic potential energy (0) | 2024.05.28 |
| 3. Electric flux (0) | 2024.05.22 |
| 2. Electric Field (0) | 2024.05.15 |



