1. Functional specification of circuit
우리는 combinational system의 functional specification으로 truth table을 사용할 수 있다. Specification하는데 있어서 불필요한부분을 제거하고 명확하게 기능을 기술한다

Table의 row는 $2^n$ 이므로 입력값이 많아질수록 row의 길이가 너무 길어지는 문제점이 있다.
또 다른 방법으로 boolean expression을 사용할 수 있다.

위의 식은 sum of product 형태이며, 입력의 조합을 각각 넣고 계산하여 truth table로 변환될 수 있다.
반대로, truth table을 sum of product형태의 boolean expression으로 변환할 수 있다.
예를 들어, 위의 OR에 해당하는 truth table에서 OUTPUT이 1에 해당하는 row를 뽑고, INPUT이 0인것은 NOT을 붙이고, 1인것은 그대로 하여 곱한다(Product). 그리고 각각 row에 대해서 그것들을 실행하고 각각 더한다(Sum).
따라서, 다음과 같이 표현된다. $Y = \overline{A}B + A \overline{B} + AB$
이러한 sum of product 형태의 functional specifation을 implement하기 위해서, INVERTER, AND, OR logic gate를 사용할 수 있다.
2. N-input logic gate
ABCD boolean expression을 구현하는 4-input gate을 구현한다고 해보자.
AND연산은 associative(연산순서와 무관, 결합법칙만족)하므로 (AB)(CD), (((AB)C)D) 와 동일하며, 따라서 아래와 같이 구현될 수 있다.

두가지 모두 gate의 갯수가 동일하여 cost가 동일하다고 가정하면, 위는 tree 구조로 propagation delay가 logarithmically 하게 증가하지만, 아래는 chain구조로 linearly하게 증가한다. 따라서, 위의 tree구조가 더 낫다고 볼 수 있다.
또한, 우리는 AND/OR gate가 아닌 NAND gate나 NOR gate로 구현하는 것이 더 좋은데, 왜냐하면 CMOS gate는 기본적으로 최종 출력이 inverting되는 naturally inverting이기 때문이다. AND의 구현은 실제로 inverter를 더 붙여서 구현해야 한다.

하지만, NAND와 NOR은 associative하지 않으므로, chain이나 tree 구조로 연결하여 n-input NAND/NOR을 사용할 수가 없다. 참고로, NAND, NOR은 univeral gate이다. NAND, INVERTER 만으로 모든 fnction을 구현할 수 있다.
위의 2-input NAND gate처럼 n-input NAND의 pulldown network는 NFET n개가 series로 연결되어있다. Input의 갯수가 많아질수록 parallel로 연결된 PFET의 capacitance값이 증가(C = C1 + C2 + ...)하고, series로 연결된 NFET의 resistance값이 증가(R = R1 + R2+ R3+...)하게 된다. 따라서 시간상수 $\tau$ 가 증가하여 propagation delay가 크게 증가하게 되며, resistance 증가에 따른 voltage drop을 야기할 수 있다.
따라서, 적은 input을 사용하는 gate를 Tree구조 등으로 조합하여 사용함으로서 하나의 gate에 input의 갯수를 제한하는 것이 좋다. 하지만, Circuit의 size가 커지고, 구성이 복잡해진다는 단점이 있으므로 이를 적절히 trade-off 하여 설계해야 한다.
3. NAND/NOR gate conversion
NAND gate를 NOR gate로 바꿔줄 경우, NAND gate의 input들을 invert시킨 NOR gate로 바꿔주면 된다.

NOR gate를 NAND gate로 바꿔줄 경우, NOR gate의 input들을 invert시킨 NAND gate로 바꿔주면 된다.

위와 아래의 기능은 동일한데, NAND가 NOR보다 propagation delay가 적어서 좋지만, NOR circuit을 사용하는 장점도 존재한다.
NAND circuit의 경우 input A가 gate 2개 연결되어, 충전/방전을 해주어야 하는 반면,
NOR circuit의 경우 input A가 gate 1개에 연결되어 충전/방전을 해주고, Inverter에 의한 빠르고 정확한 V_DD, GND 출력을 gate 2개에 연결시켜 충전/방전을 해주므로 훨씬 빠르고 명확한 신호전달을 할 수 있다 .
4. Logic simplification
sum of product 형태로 표현된 boolean expression은 boolean algebra를 이용하여 simplification가 가능한데 아래 표를 참조하면 유용하다.
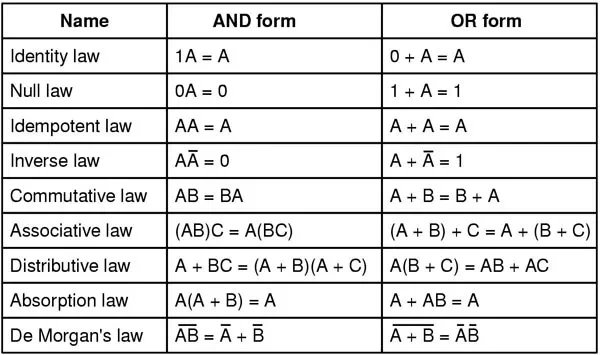

예를 들어, 위의 식은 $Y = \overline{C}A + CB$ 로 simplification 할 수 있다.
Truth table에서도 공통된 부분을 X (don't care variable) 로 표기함으로서 row 갯수를 줄여 표현할 수 있다.
이를 circuit으로 구현하면, 다음과 같이 표현될 수 있다.
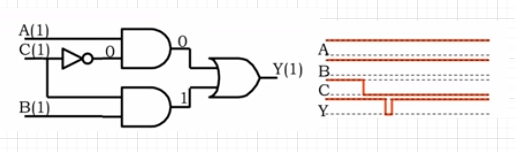
C가 0으로 떨어질 때, propagation delay의 차이 때문에 순간적으로, 아래의 gate가 먼저 0이 되어 Y의 출력이 0으로 떨어지는 현상이 발생하는데 이를 glitch라고 하며, 이것을 피하고 lenient하게 구현하기 위해 다른 boolean expression으로 바꾸어 구현 하는 것이 좋다
5. Karnaugh Maps
Karnaugh maps은 truth table을 matrix의 형태로 표현하여, truth table의 공통된 부분인 X를 쉽게 찾도록 한다. 이를 통해 빠른 simplification이 가능하며, 각 cell에 cyclic하게 인접한 cell들은 1bit만 차이 나도록 구성되어있다.
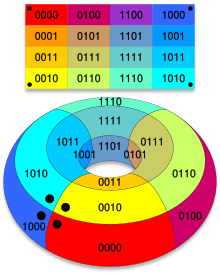
만약, 5개 이상의 variable에 대해서 karnaugh map을 구성하려면 2-dimension matrix가 아닌 3-dimension matrix로 구성하고 simplification을 해야하지만 직관적으로는 쉽지가 않다. 하지만, 더 높은 dimension에 대해서도 K-map의 simplification방식은 여전히 적용가능하다.
Karnaugh Map의 simplication방식은 Implicants를 찾는 것이다.
Implicant란, 1, 2, 4 등 2의 배수의 width&length 를 갖는 rectangle region이며 값은 모두 1이여야 한다.
Implicant끼리는 overlap될 수 있으며, prime implicant는 다른 implicant로부터 완전히 포함되지 않는 implicant이다.
우리는 prime implicant들으로 sum of product의 형태의 boolean expression을 찾을 수 있다.
Implicant가 클수록 더 작은 product term을 얻는다.
| CD\ AB | 00 | 01 | 11 | 10 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 |
위의 Karnaugh mape을 통해서 다음을 얻는다. $ Y = \overline{B} + \overline{A}C$
이렇게 추출된 SOP(sum of product)는 가장 간소화된 SOP형태가 된다.
6. Multiplexer
Multiplexer는 여러개의 input중 하나를 선택하여 output으로 보내는 switching 장치이다.
위의 그림에서, S0, S1, S2 총 3비트에 의해서, A ~H 까지 어떤 input을 Z로 내보낼지가 결정된다.
MUX는 universal gate로, 2-to-1 mux에 input을 연결시켜 AND, OR, NOT gate로 동작시킬 수 있고, 어떠한 logic function도 구현할 수 있다. 이러한 유연성 기능적 완전성을 이유로 MUX를 natural gate라고 한다.
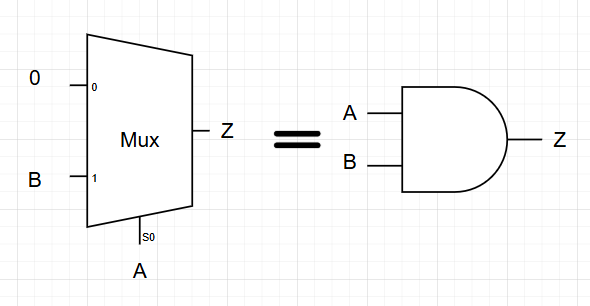
7. Decoder & ROM(Read-only-memory)
Decoder는 MUX와 반대로, N개의 input이 주어졌을 때 2^N개의 output중 하나를 선택하여 output으로 내보낸다.
ROM은 decoder를 이용하여 구현할 수 있는데, 가령 memory의 주소값을 input으로 넣어 해당하는 데이터인 output을 출력하도록 할 수 있다. 하드웨어적으로 설계되어 전원이 꺼져도 데이터를 유지한다.
ROM의 matrix size는 오직 input과 output의 갯수로 정해진다.
수정가능한 ROM circuit으로 구현한 것은 truth table이 나타내는, function specification에 독립적이다. 즉, circuit의 manufacturing이후에도, truth table의 output row 중 하나가 변경되었다면, 전체적인 circuit구조를 유지한채로 해당 부분 circuit line만 다시 reconfiguration하면 된다. 전체 circuit을 다시 재설계할 필요가 없다는 뜻이다.
'프로그래밍 > Computer Structure' 카테고리의 다른 글
| 4. CMOS(Complementary Metal-Oxide-Semiconductor) - 2 (0) | 2024.11.12 |
|---|---|
| 3. CMOS(Complementary Metal-Oxide-Semiconductor) - 1 (0) | 2024.11.05 |
| 2. Digital Abstraction (1) | 2024.10.19 |
| 1. Basics of information (0) | 2024.10.09 |




