1. Information이란?
Information이란, uncertainty를 resolve하며 주고받는 data를 말한다(Claude Shannon, 1948)
Uncertainty를 더 많이 resolve 할수록, 더 많은 information이 전달되는 것이다.
예를 들어서, card를 랜덤으로 선택하고 card에 대한 정보를 준다고 해보자.
1) 카드는 하트이다.
2) 카드는 다이아몬드 킹이다.
1은 13개의 가능성을 남아있게 하고, 2는 오직 1개의 가능성을 남아있게 한다.
따라서, 2가 더 많은 정보를 전달한다.
2. Qantifying information
우리가 어떠한 값 $x_i$를 받았을 때, 해당 값이 나올 확률을 $p_i$이라면 받은 정보는 $I(x_i) = log_{2}(\frac{1}{p_i})$이다.
예를 들어, '카드는 하트이다'라는 정보를 받았으면, 이러한 값이 나올 확률은 13/52이므로,
$I(data) = log_2 (32/14) = 2bits$이다.
'스페이드 에이스가 아니다'라는 정보를 받았을 때, 이러한 값이 나올 확률은 51/52이므로,
$I(data) = log_2 (52/51) = 0.028bits$이다.
3. Entropy
Entropy H(X)란, random variable의 집합 X에 중에 선택되어 전달되는 data의 평균적인 information의 양이다.
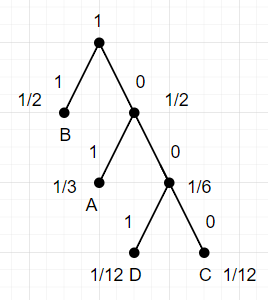
예를 들어, 전달되는 데이터 집합 X = {A, B, C, D} 이고, 각각이 나올 확률 $p_i$는 A = 1/3, B = 1/2, C = 1/12, D = 1/12라고 해보자.
각각이 나올 확률에 information의 양을 곱하고, 그것을 모두 더하면 되므로
$H(X) = E(I(X)) = \sum_{i=1}^{N} p_i log_2 (\frac{1}{p_i})$를 구하면,
H(X) = (1/3)(1.58) + (1/2)(1)+2(1/12)(3.58) = 1.626bits 이다.
전송시 Entropy에 해당하는 크기의 data를 평균적으로 보내는 것이 가장 보내는 bits의 부족함이나 낭비없이 이상적이다.
4. Encoding
Encoding이란 possible data set과 bit strings 간의 unambiguous mapping이다.
예를 들어, X = {A, B, C, D} 이고, 각각의 요소를 Encoding해보자.
| A | B | C | D | 'ABBA' | Description |
| 00 | 01 | 10 | 11 | 00 01 01 00 | fixed-length |
| 01 | 1 | 000 | 001 | 01 1 1 01 | variable-length |
| 0 | 1 | 10 | 11 | 0 1 1 0 | variable-length but, ambiguous! |
variable-length encoding은 A, B, C 등 각 symbol이 나올 확률이 다를 때 유용하지만, unambiguous하게 encoding되어야 한다. 위의 예시처럼 0110은 decoding시, ABBA, ABC, ADA 중 무엇인지 ambiguous하다.
한가지 유용한 Encoding방법은 이것을 binary tree로 표현하는 것이다. binary tree로 표현했을 때 모든 symbol은 leaves가 되어야 한다.

5. Fixed-length Encoding
Fixed-length Encoding은 symbol이 선택될 확률이 모두 동일할 때 사용한다.
Entroy는 $p_i = 1/N$ 이므로, $log_2(N)$이다 (N은 symbol의 갯수)
Binary tree의 leaves는 모두 depth가 동일하게 된다.
예를 들어, 4-bit binary-coded decimal(BCD) digits 의 경우, $log_2(10) = 3.322$ 이므로, 4bits string으로 10진수 symbol set을 mapping할 수 있다.
6. Signed Integers - 2's complement
임의의 bits string의 2's complement를 구하는 방법은, 모든 bits를 반전시키고(1's complement) 1을 더하는 것이다.
예를 들어, 11000의 2's complement는 00111 +1 = 01000이다.
원래의 수와 2's complement의 합은 0이다.
위의 예시에서, 11000 + 01000 = 100000 이고, 자릿수를 벗어난 1은 버리므로 0이 된다.
따라서, 어떤 수의 2's complemnt는 해당 수에 -를 취한 값과 동일한 의미가 된다.
이를 이용하면, 음수를 bits string을 이용해서 표현할 수 있고, high-order bit가 sign bit로서 부호를 결정하게 된다.
high-order bit가 1이면 음수, 0이면 양수이다.
예를 들어, 10010 이라는 값을 생각해보자. 이 값은 음수이고, 2's complement는 01101 + 1 = 01110 이다.
2's complement가 13이므로, 10010은 -13임을 알 수 있다.
왜냐하면 2's complement와 더했을 때 0이 되어야 하기 때문이다.
2's complement 표현을 이용하면 우리가 덧셈이나 뺄셈(-값을 더한것으로 봄) 을 할 때 어떠한 추가적 조작없이 단순이 두 bits string을 더함으로 구할 수 있게 된다.
7. Variable-length Encodings
bits를 효율적으로 사용하기 위해, higher probability를 가진 symbol은 더 적은 수의 bits를 사용하고, lower probability를 가진 symbol은 더 많은 bits를 사용하게 한다. 참고로, 데이터 전송시 반드시 평균적으로 Entropy이상의 bits를 사용해야 하도록 Encoding해야 한다(lower bound).
8. Huffman's Algorithm
Huffman's Algorithm은 optimal variable-length encoding을 구현하는 알고리즘이다.
1) 가장 나올 확률이 적은 두 symbol을 선택하여 subtree를 생성
2) 가장 나올 확률이 적은 두 symbols/subtrees를 선택하여 새로운 subtree를 생성
3) 2의 과정을 반복하면 optimal tree가 생성
그렇다면, 이것 보다 더 나은 방법이 없을까? 그렇지 않다.
더 효율적인 encoding을 위해서는 sequence of choices를 하나의 symbol로 보고, huffman's algorithm을 사용하여 encoding을 진행할 수 있다. 대부분의 File compression에서 사용하는 방식이다.
예를 들어, AA=1/9, AB=1/6, ... , DD = 1/144 이런식으로 놓고 huffman's algorithm을 사용하는 것이다.
9. Error Detection and Correction
1) Hamming Distance
Hamming Distance란, 같은길이의 두 encoding사이에서 bit가 다른 부분의 갯수를 말한다.
예를 들어, 011001과 010101은 두 부분이 다르므로 hamming distance = 2 이다.
우리의 Encoding방식의 문제점은, valid code 전송시 하나의 bit error가 다른 valid code로 해석된다는 것이다.
2) Single Error Detection
1bit error를 탐색하는 방법은 parity bit를 임의의 길이의 message에 추가하는 것이다.
1bit를 전송하는 예를 들어보자.
1의 갯수가 짝수가 되도록 parity bits를 추가한다면, 0을 보낼시에는 00, 1을 보낼시에는 11을 보내게 된다.
따라서 valid code는 00, 11이 된다.
만약 1bit error가 발생하여 10 또는 01이 수신되었을 경우에는 유효하지 않은 값이므로 1bit error가 발생했음을 확인할 수 있다. 하지만, 2bit error는 탐지할 수가 없는데, 00을 보낼시 11로 받게 된다면 11또한 valid code이므로 전송에러임을 알수가 없기 때문이다.
3) Multi-bit Error Detection
E bits의 error을 detect하기 위해서는, 코드간에 최소 E+1 bits의 Hamming distance를 갖도록 전송해야 detect 가 가능하다.
1bit를 전송하는 예를 들어보자.
위에서 우리는 1bit를 추가하는 것만으로는 2bit error를 탐지할 수 없음을 확인하였다.
그리고 위의 정리에 따르면, 2bits를 detect하기 위해서는 코드간에 최소 3bits Hamming distance가 필요하므로
0을 000 으로 전송한다면, 1은 111로 전송되어야 한다.
E bits의 error을 correct하기 위해서는, 코드간에 최소 2E+1 bits의 Hamming distance를 갖도록 전송해야 correct가 가능하다.
1bit error를 correction하기 위해서, 코드간에 3bits hamming distance를 갖도록 해보자.
0을 000으로 전송시에, 001, 010, 100 이 온 경우에는 모두 000으로 교정하고, 110, 011, 101이 온 경우에는 111으로 교정한다.
2bit error를 correct하는지 확인해보자, 000이 110으로 변경된 경우 111로 교정되므로, 제대로 correct하지 못한다.
즉, 2bit error가 발생한경우는 제대로 correct가 불가능하다.
'프로그래밍 > Computer Structure' 카테고리의 다른 글
| 5. Combinational logic (0) | 2024.11.18 |
|---|---|
| 4. CMOS(Complementary Metal-Oxide-Semiconductor) - 2 (0) | 2024.11.12 |
| 3. CMOS(Complementary Metal-Oxide-Semiconductor) - 1 (0) | 2024.11.05 |
| 2. Digital Abstraction (1) | 2024.10.19 |



