1. Introduction
Substring search란 길이 N의 텍스트에서 길이 M인 패턴을 찾는 것이다.
스팸메일을 찾거나, 유저의 입력으로부터 URL이나 RSA키를 찾는 것, 웹 스크레이핑 등 여러가지 문제를 푸는데 응용된다.
2. Brute force Algorithm
Brute force는 모든 경우에 수에 대해 하나씩 하나씩 검사하면서 패턴이 존재하는지 찾는 방법이다.
예를 들어, 입력값이 ABACAD이고, CAD인 패턴을 찾고싶다고 해보자.
ABA, CAD를 비교한다. 일치하지 않으므로 다음으로 넘어간다.
BAC, CAD를 비교한다. 일치하지 않으므로 다음으로 넘어간다.
ACA, CAD를 비교한다. 일치하지 않으므로 다음으로 넘어간다.
CAD, CAD를 비교한다. 일치하므로 찾은 것이다.
이 방식의 문제점은 입력값의 모든 M길이의 Sequence를 N번 비교하므로 성능이 MN이라는 것이다. 또한, 위의 예에서처럼 ABA를 비교완료했음에도 BA는 값을 유지시켜야 다음 BAC와의 비교를 수행할 수 있으므로 backup이 필수적으로 일어나야 한다는 문제가 있다. 따라서 buffer를 유지시켜야 한다.
2. Knuth-Morris-Pratt(KMP) Algorithm
Knuth-Morris-Pratt 알고리즘을 수행하기 위해서는 DFA라는 Deterministic Finite state Automaton(DFA)을 작동시켜야 한다. 이것은 유한한 상태를 가지며, 특정한 변화가 주어졌을 때 어떤 상태로 변화될지가 이미 결정되어져 있다.
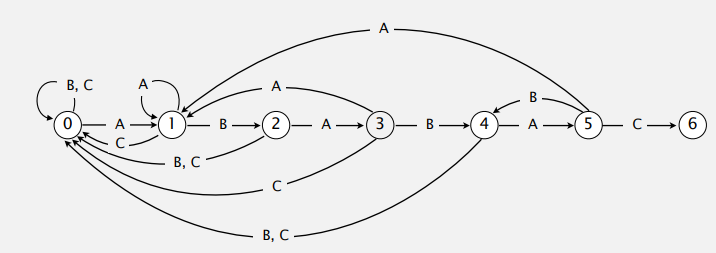
그래프로 표현하면 위와 같다. 0~6까지의 상태와 이미 결정된 상태전이 방식이 표현되어져있다.
0은 초기상태의 위치고, 6의 상태로 도달하게 되면 패턴을 찾은 것이다.
이것을 표로 표현할 수도 있는데 아래와 같다.
| A(0) | B(1) | A(2) | B(3) | A(4) | C(5) | |
| A | 1 | 1 | 3 | 1 | 5 | 1 |
| B | 0 | 2 | 0 | 4 | 0 | 4 |
| C | 0 | 0 | 0 | 0 | 0 | 6 |
첫번째 행의 ABABAC는 현재비교하는 패턴문자(상태)를 나타낸다.
첫번째 열의 ABC는 Radix를 나타낸다.
표안의 숫자는 각각 이동해야할 상태를 나타낸다.
예를 들어, 현재상태가 A(0)이고, 비교하는 입력문자가 A일 경우 대응하는 값은 1이므로 B(1)으로 이동한다.
입력값이 ACAABABACA라고 해보자.
첫번째 입력값은 A이고 상태는 A(0)이다. 표에 따라 B(1)로 이동한다
다음입력값은 C이고 상태는 B(1)이다. 표에 따라 A(0)로 이동한다
다음입력값은 A이고 상태는 A(0)이다. 표에 따라 B(1)로 이동한다
다음입력값은 A이고 상태는 B(1)이다. 표에 따라 B(1)로 이동한다
다음입력값은 B이고 상태는 B(1)이다. 표에 따라 A(2)로 이동한다
다음입력값은 A이고 상태는 A(2)이다. 표에 따라 B(3)로 이동한다.
다음입력값은 B이고 상태는 B(3)이다. 표에 따라 A(4)로 이동한다.
다음입력값은 A이고 상태는 A(4)이다. 표에 따라 C(5)로 이동한다.
다음입력값은 C이고 상태는 C(5)이다. 표에 따라 상태6으로 이동한다. 패턴찾기가 완료되었다.
그렇다면, DFA는 어떻게 생성할까? 1 -> 2 -> 3 -> 4 -> 5 -> 6 으로의 상태전이는 생성하기 쉬워보인다.
위의 예시에서 C(5)상태에서 입력값이 B인 경우를 생각해보자.
이 경우 앞의 것들은 이미 매칭이 완료가 되었기 때문에 현재까지의 입력값은 ....ABABAB인것이 확정적이다.
C(5)와 B는 매칭이 안되므로, 다음비교순서는 BABAB... 이고 다음은 ABAB....순서일 것임이 확정적이다.
그런데 여기서 우리는 BABAB는 패턴과 매칭되지 않고, ABAB가 우리의 패턴과 매칭됨을 이미 알고있다.
따라서, 상태를 A(4)로 보내서 이미 ABAB는 패턴 매칭이 확정임을 비교없이 결정지을 수 있고 다음단계를 진행할 수 있다.
결과적으로 DFA가 암시적으로 이러한 정보를 가지고 있기 때문에 가능한 것이고, 이런 원리로 DFA를 생성 할 수 있다.
결과적으로 단순히 길이 N인 텍스트가 주어졌을 때 모든 문자를 한번씩만 Access하므로, M + N 의 character access를 넘지 않는다.
한가지 문제점은 DFA를 위해 여전히 추가적인 공간을 사용한다는 점인데, Radix가 R이고 패턴의 길이를 M이라고 했을 때, 위의 표에서 처럼 RM의 추가적인 공간을 사용한다.
3. Boyer-Moore Algorithm
Boyer-Moore 알고리즘은 패턴에 매칭되지 않을 때, 최대한 많은 문자들을 Skip함으로서 성능을 향상시킨다.
이러한 skip의 계산은 길이 R인 배열을 유지시킴으로서 구현할 수 있다.
기본적으로 Brute force의 방식을 기반으로 하지만 skip의 효과는 상당한데, 평균적으로 ~N/M 의 character compare만으로 패턴을 찾을 수 있다. 패턴문자의 길이가 길수록 성능이 올라간다는 특징이 있다.
하지만, 여전히 Brute force의 방식을 기반으로 하므로 skip을 하지 못할 경우 worst case에서 ~MN의 성능을 보여준다는 단점이 있다.
KMP를 활용하여 두가지를 조합해서 사용할 경우 worst case 성능을 ~3N까지 끌어올릴 수 있다.
4. Rabin-Karp Algorithm
Rabin-Karp 알고리즘은 기본적으로 입력문자열과 패턴의 Hash값이 같다면 패턴이 매칭된 것으로 봄을 기반으로 한다.
여기서는 적당한 prime number를 이용한 Modular hashing을 이용하는데,
예를 들어, prime number = 997, pattern = 26535 라고 해보자.
Modular hashing을 하면, Hash value는 26535 % 997 = 613이다.
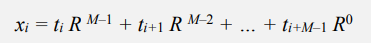
문자열의 Radix가 R이고, t가 각 위치의 character값이라고 한다면 문자열이 나타내는 값은 x가 된다.
이 때, i에 i+1을 대입한 식을 구하고 두 식을 빼면, 점화식(recurrence relation)을 구할 수 있고 아래와 같다.
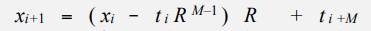
즉, 문자열이 나타내는 값 x의 hash값은 위 식이 나타내는 오른쪽 항을 hash한 값과 동일하므로, 바로 전에 비교한 문자열의 hash값을 활용하여 계산할 수 있다. 약간의 수학적 변형을 활용하면 계산과정은 매우 단축된다.
성능은 모든 패턴문자열을 비교하지 않고 일괄적으로 계산을 통해 이루어지므로, N에 비례한 linear time이 걸린다.
한가지 문제점은 Hash collision이 발생하여 false positive 판정을 할 수 있다. 즉, 패턴이 아닌데도 패턴이 매칭되었다고 보는 것이다. 하지만 실제적인 응용에서 prime number Q 충분히 큰 prime으로 설정할 경우, 몇가지 합리적인 가정하에 collision probability는 1/Q 정도 밖에 안된다.
Rabin-Karp는 두가지 버전이 있는데, 하나는 Monte Carlo version, 다른 하나는 Las Vegas version이다.
Monte Carlo version의 경우 항상 linear time임을 보장하지만, hash collision이 일어나지 않음을 보장하지 않는다
Las Vegas version의 경우 항상 올바른 답을 내리지만, linear time임을 보장하지는 않는다. Backup도 필요하다.
그렇다면, KMP나 Boyer-Moore와 같은 훌륭한 방식이 있는데, Rabin-Karp를 사용하는 이유가 무엇일까?
그것은 확장성과 관련있다. Rabin-Karp는 2차원 패턴으로 확장가능하고, 여러가지 패턴을 찾는 것으로도 확장 할 수 있다.
하지만, 성능적인 면에서는 Arithmetic operation은 character compare에 비해 느리기 때문에 평균적으로 KMP나 Boyer-Moore보다 느리다.
'프로그래밍 > Algorithm - 2' 카테고리의 다른 글
| 11. Data Compression (0) | 2024.03.03 |
|---|---|
| 10. Regular Expressions (1) | 2024.03.01 |
| 8. Tries (0) | 2024.02.25 |
| 7. String Sorts (1) | 2024.02.20 |
| 6. Maximum Flow & Minimum Cut (0) | 2024.02.18 |



