1. Strings in Java
String 는 Sequence of characters 이며, 굉장히 중요한 Abstraction이다.
C언어에서 char은 8bit integer이고, 256개의 문자를 표현할 수 있으며, 7-bit ASCII를 지원한다.
JAVA에서 char은 16bit unsigned integer이고, 16bit Unicode와 21bit Unicode 3.0을 지원한다.
Java에서 Sting type은 immutable하고, 다음과 같이 구현된다.
public final class String implements Comparable<String>{
private char[] value; //문자들
privatee int offset; //첫번째 문자가 시작하는 지점
private int length; //문자열 길이
private int hash; //cache of hashCode()
public int length(){
return length;
}
public char charAt(int i){
return value[i + offset];
}
private String(int offset, int length, char[] value){
this.offset = offset;
this.length = length;
this.value = value;
}
public String substring(int from, int to){
return new String(offset + from, to - from, value);
}
...
}
위와 같이 구현하면 substring생성시 원본인 value는 그대로 가져가고 offset만으로 문자열의 시작점을 조정함으로서 constant time에 substring생성이 가능하다. 만약 String이 아닌 StringBuilder로 구현할 경우, substring의 생성은 linear time이 걸린다. 하지만 반대로 concat()연산에서는 String은 linear time, StringBuilder는 constant time을 보인다. 이것은 어떤 구현을 선택하는지에 따라 문자열 처리 알고리즘의 성능이 달라질 수 있음을 보여준다.
2. Key-indexed counting
지금까지 모든 비교가능한 요소에 대해서, 비교기반 정렬 알고리즘의 경우 최적알고리즘은 ~NlogN임이 밝혀졌다.
하지만, 정렬을 위한 Key가 특정 집합의 요소이고, 집합의 요소의 갯수가 R개로 정해져 있다면, 우리는 비교연산기반이 아닌 다른 방식을 이용하여 성능을 더 향상시킬 수 있다.
예를 들어, 8bit character의 경우 R = 256 종류의 character로 Key의 종류가 256개로 제한되어 있다.
a[]라는 배열을 정렬할 경우, 다음과 같은 방식으로 정렬을 구현할 수 있다.
int N = a.length;
int[] count = new int[R+1]
for (int i = 0; i < N; i++)
count[a[i]+1]++; //문자별 갯수 세기
for (int r = 0; r < R; r++)
count[r+1] += count[r]; //누적합계산(정렬시 문자별 시작위치 지정위함)
for (int i = 0; i < N; i++)
aux[count[a[i]]++] = a[i]; //정렬시 문자별 위치계산하여 복사
for (int i = 0; i < N; i++)
a[i] = aux[i]; //원본으로 복사
위 알고리즘은 ~11N + 4R 횟수의 array access를 한다. 또한, count와 copy를 위한 추가 배열이 필요하므로,
추가적으로 N + R의 공간을 사용한다. 이러한 정렬방식은 R이 constant라고 생각할 경우 linear time이라고 볼 수 있다.
3. LSD radix sort (Least-significant-digit-first string sort)
Fixed-length가 W인 String를 요소로 가진 N길이의 String[]가 주어졌을 때, LSD는 least significant digit인 문자열의 맨 오른쪽부터 시작해 key-indexed counting으로 정렬시키고, 왼쪽으로 나아가면서 그러한 정렬을 반복한다. 이러한 방식의 정렬이 가능한 이유는 key-indexed counting방식의 정렬이 상대적 위치를 보존하는 Stable한 알고리즘이기 때문이다. 따라서 LSD radix sort는 stable한 알고리즘이다.
실제로 LSD에서 key-indexed counting부분의 구현은 문자별 갯수를 세는 부분에서 a[i]가 아닌 a[i].charAt(d)로 바뀌는 것이 다른데(d는 갯수를 세는 부분의 자릿수), 위에서 보았듯 charAt함수는 constant time으로 구현가능하다.
최종적으로, LSD의 성능은 2NW 임이 보장된다. 하지만 추가공간을 N + R만큼 사용하게 된다.
W가 매우 작을 경우 linear time에 가깝게 된다.
4. MSD radix sort (Most-significant-digit-first string sort)
LSD의 단점은 고정된 길이를 가진 문자열을 정렬할 때만 사용가능하다는 것이었다. MSD의 경우 문자열의 길이가 서로 달라도 정렬이 가능하다.
규칙은 다음과 같다.
1) 맨 왼쪽부터 key-indexed counting으로 count[]배열을 완성시킨다.
2) key-indexed counting으로 같은 것으로 묶인 것 끼리 recursive하게 다음 오른쪽 자릿수에 대해 key-indexed counting을 한다.

즉, 첫번째 자리부터 정렬하고, 그 다음은 첫번째 자리가 같은것끼리 모아서 두번째를 정렬하고 이러한 방식을 계속 recursive하게 반복함으로서 정렬을 완성시키는 것이다.
만약 charAt()으로 문자열길이가 넘어간 곳이 지정될 경우, count[1]에 해당하는 문자로 간주함으로서, 정렬상 맨 첫번째 순서에 지정되도록 한다. 예를 들어 sell과 sells를 비교할 경우, 5번째 자리수 비교에서 sell이 먼저 오도록 하는것이다.
MSD의 한가지 문제점은, R의 갯수만큼 subarray로 나누어서 각각에 대해 recursive하게 함수를 호출해야 하는데, 함수호출이 깊이 들어가게 되면 크기가 작지만 너무 많은 subarray를 발생시키고, 매 호출시마다 R크기의 count[]를 필요로 함으로, 성능이 느려지게 된다. 이에 대한 한가지 보완책은, recursive하게 탐색하는 과정에서 특정길이이하로 subarray가 생성될 경우, 단순히 Insertion sort를 이용하도록 함으로서 성능을 향상시키는 것이다.
다른 문제점은 메모리를 Random하게 Access하므로, cache ineffient하다는 것이다.
MSD의 성능은, Random한 순서로 String Key값을 구성하게 될 경우, 평균적으로
sublinear한
성능을 보여준다.
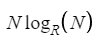
이것은, LSD와 달리 recursive에 탐색하다가 더 이상 조사할 없을 경우 문자열의 끝자리까지 조사하지 않고, 조기에 끝내버리고 모든 문자를 비교하지 않음으로 인해 발생한다. 추가공간의 경우 함수호출스택의 깊이를 D라고 했을 때 그만큼 count[]를 사용하므로, N + DR 을 사용하게 된다. 또한 key-indexed counting을 기반으로 하므로 Stable하다.
문자열의 평균적인 길이가 W일 경우에는 2NW의 성능을 보장한다. W가 매우 작을 경우 linear한 성능을 보여줄 것이다.
5. 3-way radix quicksort
3-way radix quicksort란, quick sort의 일종이다. 다만 compareTo()가 아닌 charAt() 기반이다.
먼저, 배열에서 첫번째 문자열의 첫번째 자릿수의 문자를 s라고 해보자.
해당 문자를 기준으로 첫번째 자릿수를 s보다 작은/s와 동일한/s보다 큰 이렇게 3개의 partition으로 나눈다.
s와 동일한 partition은 두번째 자릿수로 이러한 3개의 partition을 나누는 것을 resursive하게 시도하고, s보다 작은/s보다 큰 2개의 partition은 첫번째 자릿수로 3개의 partition을 나누는 것을 resursive하게 시도 한다.
이러한 방식은 count[]를 유지시키지 않으므로 추가공간을 logN + W 를 사용하고 , key-indexed counting기반이 아니고 quick sort기반이므로 non-stable이라는 단점이 있다. 성능의 경우, quick sort와 같이 랜덤하게 KEY를 구성할 경우 약 1.39NlogN의 성능을, 문자열의 평균적인 길이가 W일 경우에는 1.39WNlogR의 성능을 보장한다. W와 R이 매우 작을 경우 linear한 성능을 보여줄 것이다.
MSD와 달리 cache-friendly하다는 장점이 있다.
6. Suffix arrays
매우 큰 길이의 장문의 텍스트 파일이 있다고 해보자. 그리고 여기서 가장 많은 빈도로 반복되는 문자열을 찾고싶다고 해보자. 어떻게 찾을 수 있을까? suffix sort를 이용하여 해결할 수 있다.
먼저, input string를 이용해 0번 suffix, 1번 suffix, .... N번 suffix를 만든다(N은 input string길이)
예를 들자면, input string이 verygoodverygood이라면 다음과 같다.
0 verygoodverygood
1 erygoodverygood
2 rygoodverygood
...
6 dverygood
7 verygood
8 erygood
...
14 od
15 d
그리고 이것에 대해서, radix sort를 하여 동일한 부분을 찾아내면 손쉽게 구할 수 있다.
그렇다면 이번에는 가장 긴 길이의 반복되는 substring을 찾고싶다고 해보자.
여기서 나오는 한가지 문제는, 매칭되는 substring의 길이 D가 너무 길 경우 D^2에 비례하는 quadratic비교가 일어난다는 점이다.
위의 예시에서, longest repeated substing은 verygood인데, 비교는 d에서, od에서, ood에서... erygood에서, verygood에서
일어나게 되므로, 1+2+3+...+d만큼의 비교가 일어나게 된다.
하지만 Manber-Myers algorithm을 이용한다면 linearithmic하게, suffix trees를 이용할 경우 linear하게 비교가 가능하다. Manber-Myers algorithm의 경우 비교의 자릿수를 2배씩 계속 늘려가고, inverse[]배열을 유지시킴으로서 그것을 구현한다.
'프로그래밍 > Algorithm - 2' 카테고리의 다른 글
| 9. Substring Search (1) | 2024.02.28 |
|---|---|
| 8. Tries (0) | 2024.02.25 |
| 6. Maximum Flow & Minimum Cut (0) | 2024.02.18 |
| 5. Shortest Paths (0) | 2024.02.13 |
| 4. Minimum spanning tree(MST) (1) | 2024.02.12 |

