이번 주제는 Binary search tree를 이용해 Geometric objects 간의 Intersection을 찾는 것이다.
1. 1d range search
1차원 상에서 여러가지 점들이 있을 때, 특정 범위(range)에 존재하는 점들을 찾는 문제이다.

각각의 점들의 BST에 넣고 다음,
range count(범위 내 점 갯수) 코드는 아래와 같고, rank함수는 logarthmic time이므로, range count도 그렇다.
public int size(Key lo, Key hi){
if(contains(hi))
return rank(hi) - rank(lo) + 1;
else
return rank(hi) - rank(lo);
}
range search는 root부터 시작해 current node가 찾고자하는 범위 안에 있는지 파악함으로서, left/right 노드에서 범위내 존재할 가능성이 있는 곳으로 recursive하게 탐색한다. 이것은 R + logN (R은 범위 내 점 갯수)
2. Line segment intersection
수직/수평 직선이 존재하는 2차원상에서 선들이 교차하는 지점들을 찾는 문제이다.
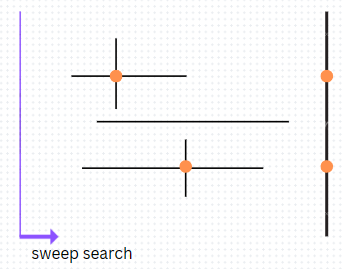
왼쪽에서 오른쪽 방향으로 sweep vertical line을 이동시키면서 수평 직선을 만날 때마다 y좌표를 BST에 넣는다.
수직 직선을 만날 때, y좌표의 범위를 1d range search함으로서, 교차하는지 여부를 찾는다. 수평직선의 오른쪽 끝에 도달할 때마다 BST에서 y좌표를 삭제한다.
N개의 선에 대해, BST삽입, 삭제, range search가 이루어지고, 성능은 NlogN + R에 비례한다.(R은 Intersection 수)
3. kd trees
1) 2-d orthogonal range search
1d range search와 다르게 2차원상에서 범위 내의 점들을 찾는 문제이다. 범위는 직사각형의 형태로 주어진다.
첫번째방법은 균등하게 나누어진 grid sqare을 설정하는 것이다.

먼저, 특정 공간을 (M x M)의 grid로 나눈다. 그리고 각각의 grid squre의 위치를 Index로하는 2차원 배열을 생성한다.
각각의 배열의 요소는 각 squre 내부 point의 list이다. 해당 범위로 표현된 직사각형을 포함하는 grid squre만을 조사함으로서, 손쉽게 값을 얻을 수 있다.
전체 공간은 MxM size의 배열을 생성하고, N개의 point들을 리스트로 넣으므로 M^2 + N 이다.
각 squre당 조사시간은 접근시간(1)에 평균적으로 조사하는 점의 갯수이므로 N/(M^2) 이므로, 1 + N/(M^2) 이다.
그렇다면 M을 얼마로 할것인지가 중요한데, 일반적으로 M^2 = N으로 설정하는, 즉 grid squre 갯수를 총 N개로 생성하여, squre당 평균적으로 1개의 point가 존재하도록 하는것이 가장 유리하다. 이럴 경우 조사시간은 constant time으로 매우 빠르다.
하지만, 한 squre에 모든 point가 집중적으로 모여있다면, squre 내부를 조사하는 시간은 N이 될 것이다. 이러한 상황 clustering은 geometric problem에서 자주 발생한다. 따라서, 이 해결방법은 점들이 균등하게 분포되어있을 때, 좋은 성능을 보여주게 된다.
두번째 방법은 공간을 나눌 때 균등한 크기의 squre로 나누는 것이 아닌, 실제 존재하는 점을 기준으로 recursive하게 나누는 것이다. 이럴 경우, clustering되어 있더라도 빠른 성능으로 탐색이 가능하다.
여러가지 방법이 있지만, BST를 활용하기 위해서 기본적으로 공간을 해당점을 기준으로 2개로 나누어 보겠다.
아래와 같은 방식으로 나누어 질 수 있다(초록색은 찾을 범위).
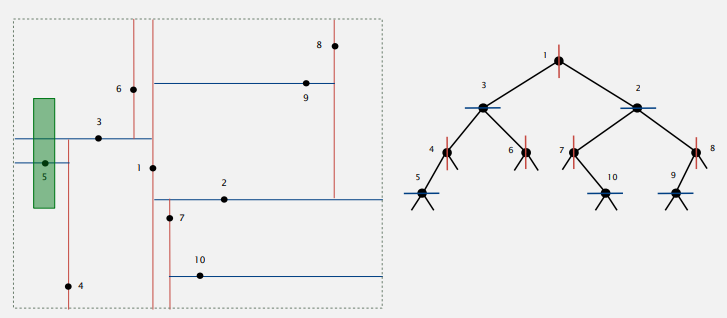
그림을 보면 각각의 node는 일반 BST의 node와는 다르게 방향정보를 가지고 있다. 수직방향 node의 left/right subtree의 node들은 항상 해당 line보다 왼쪽/오른쪽에 있다. 수평방향 node의 left/right subtree의 node들은 항상 해당 line보다 아래/위에 있다. 이런 규칙을 갖는 BST tree에 node를 삽입하고, 찾을 때는 이러한 정보를 활용해서 탐색할 필요가 없는 subtree 를 배제하는 방식으로 recursive하게 탐색한다. 평균적인 성능은 R + logN 이고, worst case에서 R + √N 이다.
해당 트리를 유지한채로 응용한다면 한 점을 기준으로 가장 가까운 이웃점을 찾는 문제 또한 동일하게 해결가능하다.
이 경우 평균성능은 logN 이고, worst case에서 N이다.
kd tree란, k차원의 공간에서 여러 점들이 존재할 때, 각각의 평면좌표계에 따라 위와 같이 2개의 공간으로 나누는 방식으로 생성된 BST이다. 예를 들자면, 3차원에서는 x-y, y-z, x-z 총 3개의 평면 좌표계가 존재하고 각각 BST가 생성되고 유지될 것이다.
4. 1d interval search
1차원 상에서 점이 아닌 interval(간격)들이 존재하고, 특정 interval과 교차하는 interval들을 찾는 문제이다.
interval은 (7, 10)과 같이 (left end point, right end point)의 형태로 주어진다.
먼저, left end point를 key로 하여 BST에 집어넣는다.
한가지 특징은 BST의 각 node들은 subtree에서 존재하는 max right end point값을 갖고 있고, insert/delete시마다 이 값은 tree를 거슬러 올라가며 recursive하게 update된다.

searching은 먼저 root(current node)부터 조사하고 해당하지 않으면 왼쪽 children node로 간다.
만약, 왼쪽 children이 null이라면 오른쪽 node로 간다.
만약, 왼쪽 children의 max right end point가 조사하는 interval의 left end point보다 작다면, 오른쪽children으로 간다.
(left children subtree의 모든 right end point가 조사하는 interval의 left end point보다 작으므로, 왼쪽은 조사할 필요x)
그렇지 않다면 그대로 왼쪽 children node로 가서 recursive하게 조사한다.
(current node의 left end point보다 조사하는 interval의 right end point가 더 작으므로, 오른쪽은 조사할 필요x)\
교차하는 하나의 interval을 찾는데는 logN, 모든 교차하는 interval을 찾는데는 RlogN 의 시간이 걸린다.
5. Rectangle intersection
2차원 공간에서 교차하는 선이 아닌 교차하는 직사각형들을 찾는 문제이다.
예전에 microprocessor 설계시에 geometric 제약사항을 준수하는지 확인하기 위해 사용했다고 한다..

교차하는 선을 찾는 문제와 같이 위의 그림처럼 왼쪽에서 오른쪽으로 sweep search를 수행한다.
다른 점은 수평선의 y좌표를 찍는 것이 아닌, 직사각형의 수직 boundary의 interval을 찍는 점이 다르다.
따라서, 이 문제는 1d interval search 문제로 변환되고, interval이 있다면 교차하는 것이 있다는 것이다.
N개의 직사각형에 대해, interval 삽입/삭제는 모두 NlogN, interval search NlogN + RlogN 의 성능을 보인다.
'프로그래밍 > Algorithm - 1' 카테고리의 다른 글
| 14. Symbol Table Applications (1) | 2024.01.16 |
|---|---|
| 13. Hash tables (1) | 2024.01.08 |
| 11. Balanced Search Tree (1) | 2024.01.03 |
| 10. Symbol tables & Binary search trees(BST) (0) | 2024.01.01 |
| 9. Priority Queue (1) | 2023.12.26 |

