알고리즘을 분석하는 것은 여러 이해관계자의 관점에서 중요하다.
프로그래머는 코드를 개발하기 위해, 고객은 효율적으로 문제를 해결하기 위해, 이론가는 동작을 이해하기 위해 필요하다. 알고리즘을 분석한다는 것은, 우리가 프로그램이 어떻게 동작할 것인지 예측가능하게 하고, 여러 추후에 발생할 수 있는 문제들에 대해서 대비하고 대처할 수 있게 한다.
알고리즘의 성능을 예측하고 비교할 수 있는 한가지 프레임워크는 다음과 같다.
Observe -> Hypothesize -> Predict -> Verify -> Validate
3-SUM 문제를 생각해보자. 이 문제는 N개의 요소를 가진 배열이 존재할 때, 서로 다른 3개의 요소의 합이 0이 되는 것이 몇 개나 존재하는지를 세는 문제이다.
1) Empirical analysis (경험적 분석)
아래는 Brute-force알고리즘으로 3-SUM문제를 해결 할 때, 실행시간을 측정한 예시이다.
N의 갯수 2배씩 증가시켜 실행시간을 측정하고 N의 갯수에 따른 그래프를 그린다. (Observe)
| N | time (seconds) |
| 250 | 0.0 |
| 500 | 0.0 |
| 1000 | 0.1 |
| 2000 | 0.8 |
| 4000 | 6.4 |
| 8000 | 51.1 |
| 16000 | ? |

그래프의 기울기가 선형적으로 증가하지 않으므로 양쪽에 log를 씌워 log-log plot을 만든다.

그래프의 모양이 선형적으로 변했고, 1차함수로 모델링할 수 있다. (Hypothesize)

따라서, 위와 같은 다항함수일 것이라고 예측할 수 있고(Predict), 이후 N = 16000일 때, 408.1s가 걸리는 것을 확인함으로서 모델이 타당하다는 것을 확인한다.(Verify) 이러한 과정을 반복적으로 실행함으로서 해당 모델이 유효함을 검증한다.(Validate)
일반적으로 해당모델에서 지수부분은 System Independent한 Algorithm, Input Data에 의해 결정되고,
상수부분은 System Dependent한 Hardware, Software, System 특성에 의해 결정된다.
따라서, Empirical analysis는 특정 환경에서 매우 쉽고 싸게 알고리즘의 성능을 예측 할 수 있다는 장점이 있지만, 환경에 따라 모델이 달라지므로, 다른 환경에서 어떻게 동작하게 될지 예측할 수 없다는 단점이 있다.
2) Mathematical Model
수학적 모델에서 실행시간은 모든 연산에 대해 cost * frequency를 구한 총합이다.
여기서 cost는 시스템 성능에 따라 변하고 frequency는 input data에 따라 변한다.
연산이란 선언, 할당, 비교, 배열 엑세스, 함수실행 등을 모두 포함한다
예를 들어, INPUT이 N이고 이것을 배열의 크기로 하여 1차원 배열을 할당할 때, 실행시간은 aN 으로 표현될 수 있다.
하지만 이러한 연산들에 대한 실행시간을 모두 더해서 표현하는 것보다 더 나은 표기가 바로 tilde notation이고, 간단하고 편리하므로 주로 사용한다.
f(N) = 2N^2 + 20N + 16 이라면, 이것은 g(N) = ~2N^2으로 표현 될 수 있다.
그 이유는, tilde notation으로 표현되기 위한 조건인 아래 수식을 만족하기 때문이다.

참고로 이런 이산적인 숫자의 합계의 경우, 연속적인 적분으로 근사가 가능하다.

이러한 모델은 매우 이상적이고 정확하지만, 실제로 사용되기에 너무 복잡하다는 단점이 있다.
3) Order-of-growth classifications
기본적으로 대부분 함수의 실행시간 증가율은 다음 중 하나로 표현되어도 문제없다.

특히, logN (logarithmic)은 divide in half로 해결하는 binary search 가 대표적이고
NlogN (linearithmic)은 divide and conquer로 해결하는 mergesort가 대표적인 알고리즘이다.
아까 위에서 봤던 3-sum문제의 경우 insertion sort와 binary search를 조합하면
N^2logN으로 성능이 향상된다.
4) Theory of algorithm
실행시간계산에서, cost는 알고리즘 그 자체와 input으로 결정된다고 했다.
따라서, 동일한 알고리즘이여도 input에 따라 실행시간이 제각각일 수 있다.
그래서 실행시간은 input에 따라, worst case / average case / best case 로 분류할 수 있다.
일반적으로 우리가 고려하는 cost는 average case에 해당하지만 특별히 최악의 상황을 피해야 하는 경우 worst case를 고려해야 한다.
이렇게 현재 알고리즘의 실행시간을 구했다고하자, 그런데 이게 최적의 알고리즘일까?
그것은 알고리즘의 upper bound와 lower bound로 판별할 수 있다.
예를 들어, 3-sum문제의 가장 낮은 cost를 가진 알고리즘이 현재 ~N^3 이라고 해보자.
그렇다면 upper bound는 N^3이고 O(N^3)으로 표현한다.
lower bound는 어떤 알고리즘도 이보다 더 좋아질 수 없음이 증명된 cost이다.
이것을 N이라고 해보자. Ω(N)으로 표현된다.
그렇다면 그래프로서, 아래 노란색 빗금친 영역에 최적의 알고리즘이 존재한다는 뜻이된다.
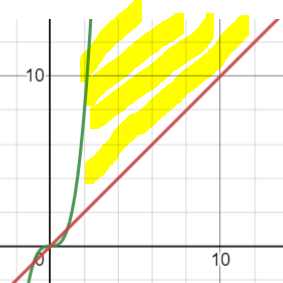
그런데, 3-sum문제의 알고리즘이 binary search를 활용해 N^2logN으로 향상되었다고 해보자
그러면 upper bound가 줄어들게 되고 최적의 알고리즘이 존재하는 범위가 줄어들게 된다.
시간이 또 지나서, 이전 증명은 잘못되었고 해당 문제는 N^2logN이상으로 더 좋아질 수 없음이 증명이 되었다고 해보자.
그러면 lower bound는 N^2logN가 되어 upper bound와 일치하게 되고, 최적의 알고리즘이 결정된다.
즉, 우리는 알고리즘 개발을 반복하고 lower bound를 증명함으로서 최적의 알고리즘을 발견할 수 있다.
하지만 이 방식의 한가지 문제점은 lower bound의 증명이 매우 어렵다는 것이다.
※메모리 사용량의 tilde notation 활용※
일반적으로 변수할당에 따른 메모리 사용량은 다음과 같다.

만약 N =10000, int[N]이라는 배열을 할당한다고하면, 혼자서 차지하는 메모리 할당량은 다른 것들에 비해 매우 클것이다.
따라서, 단순히 tilde notation으로 ~4N으로 표현될 수 있다.
'프로그래밍 > Algorithm - 1' 카테고리의 다른 글
| 6. Selection sort, Insertion sort, Shell sort (0) | 2023.12.12 |
|---|---|
| 5. Introduction of Sort (0) | 2023.12.09 |
| 4. Bag, Stack, Queue (1) | 2023.12.03 |
| 2. Union-Find (1) | 2023.11.20 |
| 1. Introduction (0) | 2023.11.20 |